(一)变量选择及理由

本文研究的重点在于工程保险发展与区域经济以及区域创新间的关系，故而将工程保险规模指标和效益指标作为被解释变量，区域经济和区域创新指标作为解释变量。

1.被解释变量的选取。本文根据研究需要，选取工程保险的保费收人和赔付支出作为被解释变量，分别用来衡量工程保险的业务规模和效益。

2.解释变量的选取。显然，被解释变量(保险收人和赔付支出)衡量了工程保险的不同维度，故而决定了本文将根据不同的被解释变量选取解释变量来进行针对性地实证分析。

在研究宏观经济对保险业规模的影响时，通常选取国内生产总值(GDP)作为宏观经济指标的典型代表引人模型当中。但由于本文的研究对象是工程保险业而非整个保险业，因此本文选取建筑业生产总值作为研究宏观经济对各地区工程保险保费收人影响时的解释变量。

在分析工程保险赔付支出的影响因素时，本文选取了专利授权数作为解释变量。由于区域创新缺乏可度量性，而Acs Anselin等论证了专利能够作为创新产出的可靠衡量指标, Feldman and Flori-da通过实证研究得出，专利与创新间的相关系数高达0.934。故而本文将专利授权数作为创新产出的替代变量，以分析区域创新与工程保险间的相关关系。

3.变量的形式。本文对保费收人(prem) ,赔付支出(claim )、建筑业总产值(CPC)、专利授权数(PATENT)的年度数据取自然对数进行处理，分别得到2008-2014年各地区lnprem,lnclaim,lnCPC,lnpatent的面板数据，以达到消除变量量纲及可能产生的递增型异方差的影响的目的。

(二)数据来源及说明

本文建模的数据来源于2009-2015年《中国统计年鉴》《中国保险年鉴》等。包括2008-2014年31个省、市、自治区保费收人、赔付支出、建筑业生产总值、专利授权数的年度数据。

(三)模型的基本形式

本文研究的核心是工程保险的区域差异化，因此拟选用面板数据进行建模分析。使用面板数据的优势在于:第一，相较于单独使用时间序列数据或横截面数据，面板数据能够反映个体间存在的异质性;第二，面板数据同时具有截面与时间两个维度，观测值明显增多，样本容量更大，从而可以提高估计的精确度。

1.面板数据模型基本形式。面板数据模型基本形式为:

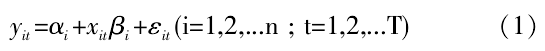
其中β_i为解释变量的系数;α_i为截距项，表现为个体影响;ε_it为自噪音。

根据α_i和β_i的不同假设，模型形式又可分为三种:

（1）不变参数模型: α_i =α_j, β_i=β_j，即截距项与斜率项是确定的。意味着可以像对待截面数据那样进行OLS回归。

（3）变截距模型: α_i ≠α_j, β_i≠β_j，即截距项不同但斜率相同。意味着存在个体影响。

（3）变系数模型: α_i ≠α_j, β_i≠β_j，即截距项与斜率项均不相同。意味着除了存在个体影响外，还存在不同的结构影响。

2.模型形式的确定。构建F统计量，利用F检验确定面板数据模型的具体形式。

(a) F检验的原假设:

其中，n代表截面数，T代表时间跨度，k代表解释变量个数。

(c)判定规则:

若F₂≤F_α [(n-1)(k+1),n(T-k-1)]，则接受H2，面板数据模型为不变参数模型;反之，则拒绝H2，继续检验Hlo

若F₁≤F_α [(n-1)(k+1),n(T-k-1)]，则接受H1，面板数据模型为变截距模型;反之，则拒绝H1，面板数据模型为变参数模型。

本文使用的计量软件是Eviews 7.2.