为了验证考虑工程扰动和地质条件的巷帮极限平衡区宽度方程的合理性与实用性，选取文献中工程实例的参数进行计算分析。文献的巷帮相关参数值见表1。

在考虑工程扰动及地质条件下，结合表1中相关参数，计算得到不同支护形式下巷帮极限平衡区宽度，与文献中的理论计算结果和实测结果对比分析，见表2.

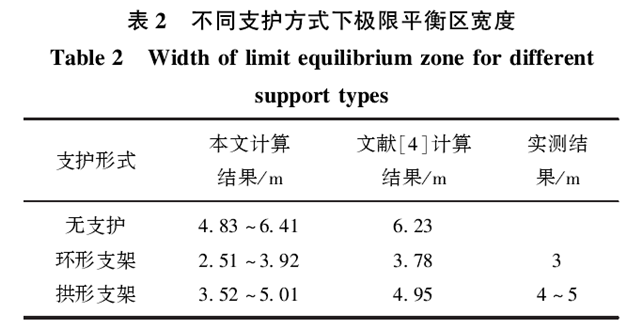
由表2对比分析可知，本文理论计算结果与前人研究成果和实测结果相吻合。另外，由于巷帮滑移面勃聚力与内摩擦角不仅与煤及其顶板岩石力学性质有关，而且与两者之间的界面平滑程度相关。因此，在一定程度上很难确定滑移面强度力学参数值，更难确定巷帮极限平衡区宽度。但在考虑工程扰动和地质强度指标条件下，确定的巷帮平衡区宽度为一个数值范围(包括了前人的单一计算结果)，避免了确定巷帮滑移面强度力学参数难的问题。因此，这里所提出的巷帮极限平衡区宽度表达式更具有普遍适用性和可行性。

结论

(1)基于广义的H-B准则与线性M-C准则，推导出了非线性岩体强度参数表达式，该表达式既克服了线性岩体强度参数的惟一性，又考虑了岩体工程扰动和地质条件，对于岩体力学参数的确定及围岩稳定性评价具有指导意义。

(2)工程扰动程度越大，岩体地质强度指标越小，岩体的节理裂隙越多，完整性较差，非线性岩体强度参数(内摩擦角、勃聚力)值越小，岩体抵抗破坏的能力越差。

(3)巷帮极限平衡区在两种极端情况下，基于建立的非线性M-C强度屈服准则，构建了巷帮滑移面正应力与极限平衡区宽度表达式，从而能确定巷帮极限平衡区的影响范围。岩体的工程扰动程度越小，岩体地质强度指标越大，岩体完整性越好，巷帮滑移面正应力值越大，巷帮极限平衡区宽度越小。

(4)通过与前人研究成果和实测结果对比分析可知，新建立的极限平衡区宽度表达式更具有普遍适用性，减小了确定巷帮滑移面强度参数难的问题。