银行间同业拆借关系是银行间传染风险形成的主要渠道之一，也是银行网络形成的关键。针对此，本节通过对银行经营行为动态刻画，构建银行内生网络模型，进而可基于此研究银行间传染风险的特征。而该类问题研究常用的模型中往往假设银行行为是静态的、同业拆借关系是外生的。因此，本文建模方法使银行行为是动态的，同业拆借关系形成是内生的，这使构建的银行系统更贴近现实情况。假设银行系统中具有N家银行，t时点银行a的总资产TAB ( t)由投资}(t}、银行间贷款IL}(t)和流动性资产Z fit)构成，总负债TL}(t>由资产净值NW}(t)、银行间借款IB}(t)和储户存款D}(t)组成。假设初始时点银行间不存在同业拆借行为，其中投资规模占总资产的比例为e，资产净资占总资产比例为Y。下面从资产更新、同业拆借和违约风险传染清算等方面，刻画银行系统动态演化过程。

(一)流动性资产与资产净值更新

根据Lux ( 2015 ) }z`}A`4的研究，假设银行储户存款变化遵循下面的随机过程

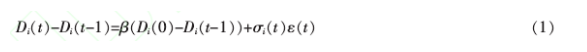
其中，参数月为常数;二‘(t卜cpTA} ( t)且。(t卜N(o}y。为了简单起见，假设1(t卜r(t })}}+R}t })}，即银行每一时点投资收益均用于下一时点投资。其中，R}(t)表示t时点银行投资收益率，R}(t)}N恤，}z }。则在t时点初期，银行i的流动性资产和资产净值分别按式(2)和式(3)进行更新。

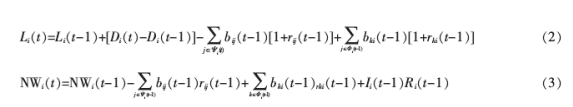
其中，}}(t)和}(t)分别为t时点银行i的债务银行和债权银行的集合;气(t)和r;; ( t)分别为t时点银行i向银行j借贷额度及其相应的利率。

(二)银行同业拆借决策机制

假设银行i的流动性临界值为Zit)-BA}t)，如果NW}t)>0且L}(t)<L}(t)，则银行i流动性短缺，且其流动性需求为z,}(t卜z fit)。如果NW}(t卜。且L}(t卜z fit)，则银行i流动性过剩，且其可提供的流动性为L}(t>_L}(t)。借鉴Riccetti等的研究，假设t时点银行a向银行.7借款的利率:}(t)为

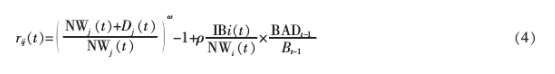
其中，BAD}_，表示t-1时点银行系统中总的坏账规模;及_，是t-1时点银行系统中同业拆借总规模;。和P为常数

流动性短缺银行同业拆借决策机制:在t=1时，流动性短缺银行随机选取一定比例M的流动性过剩银行为潜在的债权者，并观察它们提供的同业拆借利率，选择利率最低的流动性过剩银行进行同业拆借。如果此流动性过剩银行无法满足其流动性需求，其将按同业拆借利率最低原则依次向选择的其他流动性过剩银行进行拆借，直到其流动性得到满足或者没有多余的流动性可提供为止。

流动性过剩银行同业拆借决策机制:如果流动性过剩银行流动性规模大于向其申请贷款的流动性短缺银行的流动性需求，则其满足流动性短缺银行的流动性需求。否则，其按照流动性短缺银行的资产净值从大到小的顺序依次分配其流动性直到流动性分配完为止。

之后每一期流动性短缺银行依然选取一定比例M的流动性过剩银行，但其观测选取的银行和在本期流动性过剩的上一期债权银行的利率，以低利率为原则，构成一定比例M的潜在债权者集合，按照t=1时的规则向此潜在债权者集合进行同业拆借。流动性短缺银行和流动性过剩银行按照上述机制进行同业拆借，拆借完成后相应银行进行资产负债更新。此时若流动性短缺银行流动性没有得到满足，本文视其为违约。在整个同业拆借过程中，只有当流动性短缺银行能够获得必要的资金以使其满足流动性临界值条件，资金才会由流动性过剩银行为其提供，最终形成银行间同业拆借关系。

(三)风险传染清算机制

如果NW}(t) }0，本文假设银行i违约，其导致上一时点债权银行.7的坏账损失为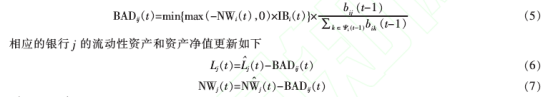

其中，z,.,-(t)与NW; ( t)分别表示银行j在t时点初的流动性资产与资产净值。如果Z,., (t) <0，则银行j因银行i违约传染而违约。本文假设违约银行由新的银行取代，且新银行资产负债表结构与违约银行的初始结构相同。