1 体育场馆的定价方法阐述

本研究通过对许多体育场馆的调查以及与场馆负责人的访谈，发现目前国内大多数体育场馆在实际定价过程中主要采用传统的边际成本定价法、目标效益定价法和需求导向试错法。

边际成本定价法:边际成本定价法主要是根据供求关系而提出的定价方式，无论需求量和供给量如何增加，只要其最优价格使消费价格与边际成本达到平衡赢利点即可。体育场馆的对外开放，必然存在运营、管理和维护等固定成本。根据经济学原理，只要存在成本就可以用边际成本分析法根据场馆折旧和管理等费用进行盈亏平衡定价研究。根据成本制定的盈亏点需要了解体育场馆对外开放每一单位的成本变化，加上场馆的折旧、管理和维护成本，结合消费人数的变化量，才能确定体育场馆的消费价格。目前体育场馆的盈利点一般设定为:场馆消费价格一固定成本/消费人数+场馆的维护、折旧和管理等固定和额外成本。这种方法的分析框架是根据供求关系和成本一利润关系所建立，相对来讲比较理想化和单一化，适合于用在儿童公园和旅游景区等的定价上。

目标效益定价法:目标效益定价法又称为目标利润定价法或投资收益率定价法。该方法的基础原理是在估算所有成本的基础上，根据目标利润率的高低来确定消费价格。体育场馆运营的成本包括投资总额分摊、人工费用、日常管理费、设备折旧费、场馆维护费及其他物料消耗费等。那么目标效益定价法就是核算场馆运营的全部成本，在保证不亏损的前提下根据目标收益确定场馆的消费定价。这种定价方法优点是简单直接、目标明确和效益保证，但该方法也存在对需求市场把握不足及过度关注经济效益等问题圈。因此，这种定价方法虽然使得场馆运营压力较小，并且能够获得较多利润，但是只有少部分愿意支付高价格的人进行消费，这与全民健身的宗旨相违背，往往会造成更多的资源浪费。

需求导向试错法:在实际情况中，由于消费偏好和习惯不同，体育场馆无论采取边际成本定价法还是目标效益定价法都无法稳定场馆消费客流，仍常常出现场馆某一时段爆满的现象，从某种角度讲场馆定价就失去了意义。因此，现在场馆定价最为普遍的是需求导向试错法，主要根据体育消费者对场馆的需求差异和强度来确定消费价格。一般根据消费时间、消费对象、消费方式和消费场地等指标来进行差异定价，比如早、中、晚和周末的消费价格各不相同，场馆会员和非会员的价格也不一样，周卡、月卡、年卡和现金的消费方式金额也不一样，最后在不断试错、保证不拥挤的情况下确定了消费价格叫。此定价方法在一定程度上可以分流消费人群，减轻场馆运营压力，但是也未能实时有效地根据现场情况动态地制定出价格，也是单一定价方法的一种。

2 体育场馆单一定价方法分析

由上可得，长期以来我国体育场馆的运营一直采取根据边际成本和目标利润等指标而单一定价的策略，就算是需求导向试错法，也是保证锻炼人数低于拥挤点的一种策略性定价方法。然而，从经济学角度讲采取单一的定价模式很难在社会福利供给和场馆经济效益之间达到有效平衡。

针对现阶段我国居民收人差距较大的状况，本研究把体育消费人群分成高收人人群和低收人人群，并且其体育消费需求曲线不同。如图1所示，若体育场馆定价过低为X,，低收人人群体育消费为士，，高收人人群消费量则为士H;若体育场馆定价过高为XI I，低收人人群体育消费为TI，高收人人群体育消费则为>I;显而易见TI,>TH>TI,>TII，故低定价不能正确反映体育消费成本，其体育消费量远远大于高定价时的总消费量，这会损坏正常舒适的体育消费体验，进而打乱体育场馆的有序运营。如图2所示，如果采取高定价策略，则会影响人们的正常体育消费福利。假设个人收人和其他消费的价格不变，用高定价取代低定价意味着:体育消费者的预算线会沿横轴逆时针移动，消费者效用最大化的均衡点也由E,移到Ez。此时随着总效用的降低，体育消费者的社会福利也随之下降，表现在消费者的无差异曲线逐步向原点移动。同时，由于低收人人群的体育消费量已经接近最低数量，因而降幅非常有限，为了支付因高定价而增加的消费成本，只好减少其它方面的消费支出，故低收人人群的社会福利损失更大目‘〕。基于分阶段博弈的游泳场馆动态定价研究  游泳场馆动态定价模型游泳馆的n可以根据场馆实际运营灵活设定。如果一个游泳馆整天的经营时长为12小时，以一个小时为一个区段，那么n =12。游泳馆根据实时的动态消费人数计算出每个区段的消费价格x;,i=l,w,n，并通过智能手机APP实时显示，然后游泳爱好者可以根据不同区段的价格来选择和预定相应的锻炼时间和场地，从而产生对应的人数为t;,i=1,...，  no

在动态显示实际消费人数t一(t1，…，tll)r,-t =-tl,"..-tn)和设定动态消费价格x一(xl，…，xl，)r--x=-xm"..-xn)的过程中，游泳馆为了追求利润的最大化，而体育消费者则追求的是锻炼成本最小化，这就相互形成了明显的动态博弈关系Ciz7。接下去，研究者就通过体育消费者和游泳馆之间的博弈关系求解出一个最优的动态定价。

首先，建立游泳馆的效用函数:

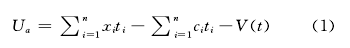
其中，C;表示第1个区段游泳馆的单个体育消费者服务成本，即边际成本(marginal cost)o  V(t)表示随着体育消费者数量的波动而造成的额外成本，定义如下:

数，系数入决定了额外波动成本的大小。因此，各区段的体育消费人数波动越大，V (t>的值也就越大。然而，目前游泳馆的效用函数U-,调整为场馆总收人减去原经营模式的服务成本和由于消费者数量波动造成的额外成本。相比原先传统的收益函数，加人额外波动成本V(t>是本研究的亮点，在以前研究成果中就已经表明如果游泳馆使用者越多，共享程度就越高，游泳场馆方所需要投人的额外成本也就越大。当然，体育消费者的目标就是在享受相同服务下，实实在在地减少体育消费成本，因此为体育消费者建立了如下效用函数:

根据数理统计和博弈论原理，游泳馆和体育消费者之间博弈的最终目的是同时达到两者效用函数的最大化，这就等同于求解数学方程式的最优化问题，故有以下方程式:

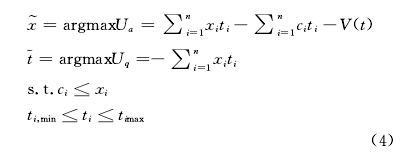
其中，_ <t,于一‘，，…，三)是最合理的区段消费价格，t. . , t)是最合理的体育消费数量。当然，为了保证方程组求解的合理性，公式(4)求解要同时满足以下两个条件:第一，为了避免游泳馆的亏本经营，区段消费价格二，不能低于场馆的基本服务成本〔、，;第二，为了保证场馆的正常经营秩序和体育消费者良好的消费环境，游泳馆区段消费人数t，不能超过其最大承载量t ;. r,--x，并且为了保证社会福利享受的公平性，t，也不能低于体育爱好者的最低合理体育消费需求。